数据结构——图

图的定义

图 (graph) 是一个二元组 $G = (V(G), E(G))$ 。

其中 $V(G)$ 是非空集，称为 **点集 (vertex set)**，对于 $V$ 中的每个元素，我们称其为 顶点 (vertex) 或 **节点 (node)**，简称点

$E(G)$ 为 $V(G)$ 各结点之间边的集合，称为 边集 (edge set)

无向图(Undigraph)

用 $(x, y)$ 表示两个顶点之间的一条边(edge)

G={V,E}，V={0,1,2,3,4,5}，E={(0,1), (0,4), (0,5), (1,2), (1,3), (1,5), (2,3), (3,4), (3,5), (4,5)}

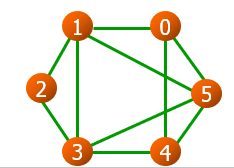
邻接点：如果 $(x, y) \in E$ ,称x,y互为邻接点，即x,y相邻接
依附：边 $(x, y)$ 依附于顶点x,y
相关联：边$(x, y)$与x,y相关联
顶点的度：n和顶点相关联的边的数目，记为TD(x)

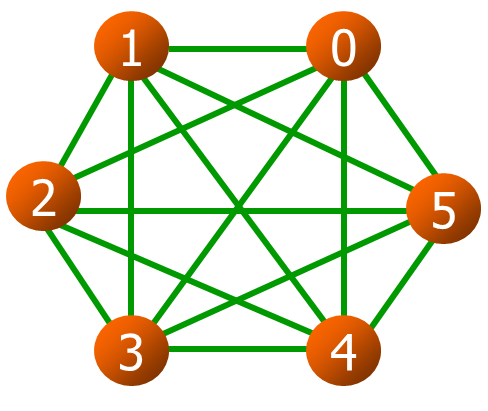
无向图 (完全图)

如果无向图有 $n(n-1)/2$ 条边，则称为无向完全图

有向图(Digraph)

用 $<x,y>$ 表示从x到y的一条弧(Arc)，且称x为弧尾，y为弧头

**G={V,E}，V={0,1,2,3,4}，E={<0,1>，<0,3>，<0,4>，<1,2>，<2,4>，<3,2> } **

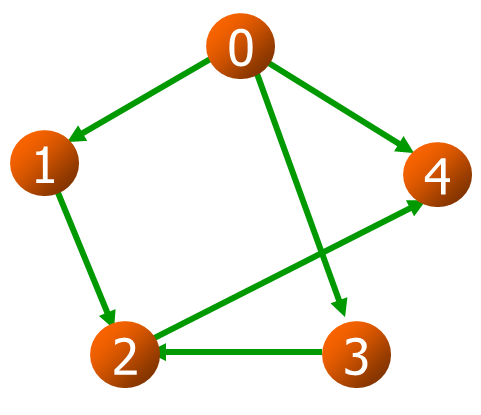
邻接：如果 $<x,y> \in E$ ,称x邻接到y,或y邻接自x
相关联：弧 $<x,y>$ 与x,y相关联
入度：以顶点为头的弧的数目，记为ID(x)
出度：以顶点为尾的弧的数目，记为OD(x)
度：TD(x)=ID(x)+OD(x)

有向完全图

如果有向图有n(n-1)条边，则称为有向完全图

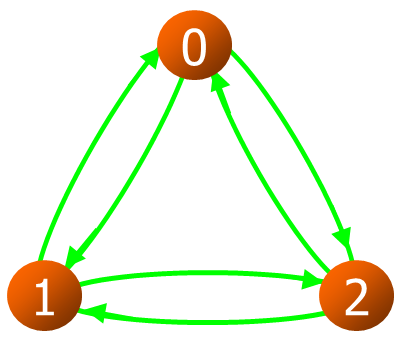
任意两个顶点之间都存在方向相反的两条弧(每个顶点和其他n-1个顶点之间有一条连线)，即$Pn^2$

网(Network)

网：带权的图称为网
权：与图的边或弧相关的数

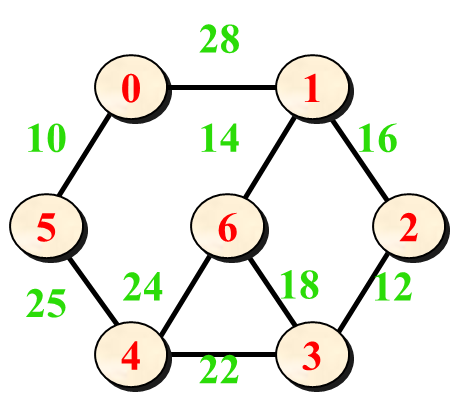
无向网的应用：最小生成树

有向网的应用：最短路径，关键路径

路径(Path)

路径：是一个从顶点x到顶点y的顶点序列(x, vi1, vi2,…, vim, y)
其中,(x,vi1),…(vij-1,vij),…(vim,y)皆属于E

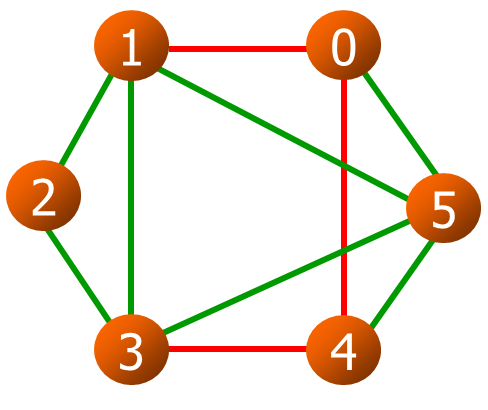
1到3有路径(1,0,4,3)

回路

回路或环：路径的开始顶点与最后一个顶点相同，即路径中 $(x, v_{i1}, v_{i2},…, v_{im}, y)$ ，x=y
简单路径：路径的顶点序列中，顶点不重复出现

连通

连通：如果顶点x到y有路径，称x和y是连通的
连通图：图中所有顶点都连通

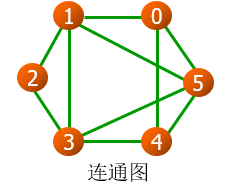
子图

设有两个图 $G＝(V, E)$ 和 $G’＝(V’, E’)$。若 $V’ \subseteq V$ 且 $E’ \subseteq E$, 称图G’是图G的子图

生成树

一个连通图的生成树是一个极小连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边

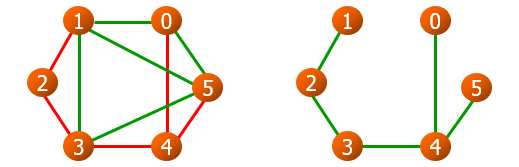
生成树是具有图中全部顶点的一个极小连通子图。一棵含有n个顶点的生成树必然含有n-1条边。

图的储存

邻接矩阵

利用一个二维数组 bool mp [N] [N]，mp [ i ] [ j ] = 1 代表E中有< i , j >这条边，而=0时则说明无这条边

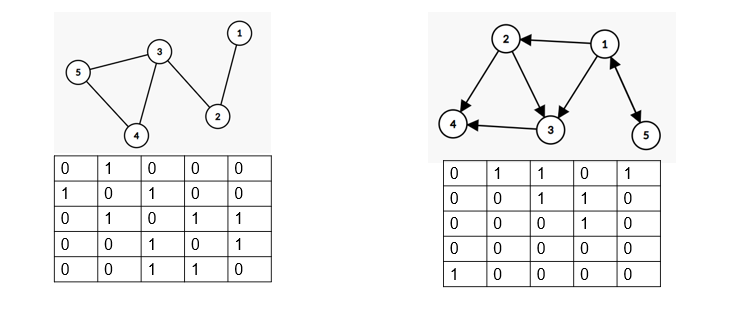
若图带权则把1换成对应的权值
无向图的邻接矩阵是对称的
A [i] [j] 可确定顶点i和j之间是否有边相连
其第i行1的个数或第i列1的个数，等于顶点i的度TD(i)
特别：完全图的邻接矩阵中，对角元素为0，其余全1。
有向图的邻接矩阵可能是不对称的
其第i行1的个数等于顶点i的出度OD(i)，第j列1的个数等于顶点j的入度ID(j)
顶点的度=第i行元素之和+第i列元素之和

代码样例：

const int MAXN = 10001;
int adj[MAXN][MAXN];
for(int i = 0; i < n; ++i){
    int u, v;
    cin >> u >> v;
    adj[u][v] = 1;
    //若无向
    //adj[v][u] = 1;
}

复杂度

查询是否存在某条边：$O(1)$ 。

遍历一个点的所有出边：$O(n)$ 。

遍历整张图：$O(n^{2})$ 。

空间复杂度：$O(n^{2})$ 。

应用

邻接矩阵只适用于没有重边（或重边可以忽略）的情况。

其最显著的优点是可以查询一条边是否存在。

由于邻接矩阵在稀疏图上效率很低（尤其是在点数较多的图上，空间无法承受），所以一般只会在稠密图上使用邻接矩阵。

邻接表

利用vector的可变长空间，我们建立vector<int>Node[N]，Node[ u ]内的任一值 v 代表有一条边 $< u , v >$

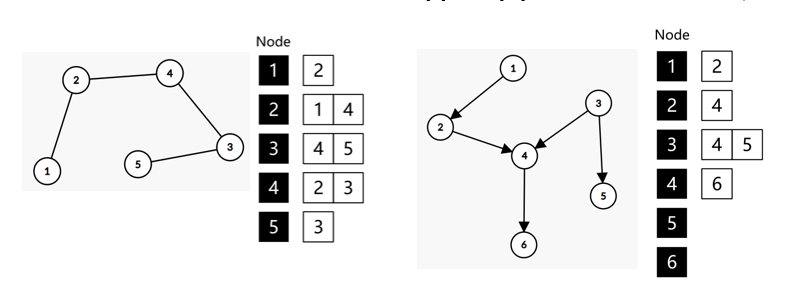
代码样例：

vector<vector<int> > adj;
for(int i = 0; i < n; i++){
	int u, v;
    cin >> u >> v;
    adj[u].push_back(v);
    //若无向
    //adj[v].push_back(u);
}

复杂度

查询是否存在到的边：$O(d + (u))$ 。

遍历点的所有出边：$O(d + (u))$ 。

遍历整张图：$O(m + n)$ 。

空间复杂度：$O(m)$ 。

应用

存各种图都很适合，除非有特殊需求（如需要快速查询一条边是否存在，且点数较少，可以使用邻接矩阵）。

尤其适用于需要对一个点的所有出边进行排序的场合。

图的遍历

从图的某一顶点开始，访遍图中其余顶点，且使每一个顶点仅被访问一次
图的遍历主要应用于无向图
遍历实质：找每个顶点的邻接点的过程。

深度优先搜索

DFS 最显著的特征在于其 递归调用自身。同时与 BFS 类似，DFS 会对其访问过的点打上访问标记，在遍历图时跳过已打过标记的点，以确保 每个点仅访问一次。符合以上两条规则的函数，便是广义上的 DFS。

邻接矩阵：

void dfs(int pos)
{
	vis[pos] = 1;
	for(int v = 0; v < n; v++){
		if(adj[u][v] && !vis[v]){
			dfs(v);
		}
	}
}

void Dfs(){
	for(int i = 0; i < n; i++){
		if(!vis[i]){
			dfs(i);
		}
	}
}

邻接表：

vector< vector<int> > graph[N];
void dfs(int u)
{
	vis[u] = 1;
	for(int v: graph[u]){
		if(!vis[v]){
			dfs(v);
		}
	}
}

void Dfs(){
	for(int i = 0; i < n; i++){
		if(!vis[i]){
			dfs(i);
		}
	}
}

广度优先搜索

BFS 全称是 Breadth First Search，中文名是宽度优先搜索，也叫广度优先搜索。

是图上最基础、最重要的搜索算法之一。

所谓宽度优先。就是每次都尝试访问同一层的节点。如果同一层都访问完了，再访问下一层。

这样做的结果是，BFS 算法找到的路径是从起点开始的最短合法路径。换言之，这条路径所包含的边数最小。

在 BFS 结束时，每个节点都是通过从起点到该点的最短路径访问的。

邻接矩阵：

void bfs(int u)
{
	queue<int> st;
	st.push(u);
	vis[u] = 1;
	while(!st.empty()){
		u = st.front();
		st.pop();
		for(int v = 0; v < n; v++){
			if(graph[u][v] && !vis[u]){
				st.push(v);
				vis[v] = 1;
			}
		}
	}
}

void Bfs(){
	for(int i = 0; i < n; i++){
		if(!vis[i]){
			bfs(i);
		}
	}
}

邻接表：

vextor<int> graph[N]

void bfs(int u)
{
	queue<int> st;
	st.push(u);
	vis[u] = 1;
	while(!st.empty()){
		u = st.front();
		st.pop();
		for(int v: graph[u]){
			if(!vis[v]){
				st.push(v);
				vis[v] = 1;
			}
		}
	}
}

void Bfs(){
	for(int i = 0; i < n; i++){
		if(!vis[i]){
			bfs(i);
		}
	}
}

图的连通性问题

无向图的连通

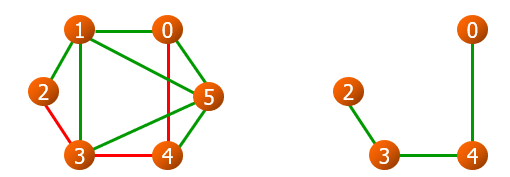
非连通图的极大连通子图叫做连通分量
若从无向图的每一个连通分量中的一个顶点出发进行DFS或BFS遍历，可求得无向图的所有连通分量的生成树(DFS或BFS生成树)
所有连通分量的生成树组成了非连通图的生成森林

最小生成树

如果无向图中，边上有权值，则称该无向图为无向网
如果无向网中的每个顶点都相通，称为连通网
最小生成树(Minimum Cost Spanning Tree)是代价最小的连通网的生成树，即该生成树上的边的权值和最小

要求：

必须使用且仅使用连通网中的n-1条边来联结网络中的n个顶点；
不能使用产生回路的边；
各边上的权值的总和达到最小。

Prim算法和Kruskal算法都可以看成是应用贪心算法设计策略的例子。

Prim算法

算法思想：从某一点出发，挑选一条连接这个点的权值最小的边，将这条边和连着的那个点加入最小生成树；

然后继续挑选一条连接目前最小生成树的权值最小的边，将这条边和连着的那个点加入最小生成树。

代码样例：

const int MAXN = 5050;
struct node{
    int to;
    int weight = MAXN;
}; 

vector<node> graph[MAXN]; //邻接表

void prim()
{
    int now = 0;
    Node tmp[len];
    for(int i = 0; i < graph[now].size(); i++){
        tmp[graph[now][i].to] = min(tmp[graph[now][i].to], graph[now][i]);
    }
    
    tmp[now].weight = 0;
    
    for(int i = 0; i < n - 1; i++){
        int min = MAXN;
        int next;
        for(int j = 0; j < tmp.size(); j++){
            if(!tmp[j].weight && tmp[j].weight < min){
                min = tmp[j].weight;
                next = j;
            }
        }
        
        for(int i = 0; i < graph[next].size(); i++){
            if(!tmp[graph[next][i].to] && graph[next][i].weight < tmp[graph[next][i].to].weight){
                tmp[graph[next][i].weight = graph[next][i].weight;
			}
        }
        
        tmp[next].weight = 0;
    }
}

Kruskal算法

算法思想：将所有边从小到大排序，然后依次挑选这些边，只要一条边连接的两个点不连通，就将这条边加入最小生成树。

具体来说，维护一个森林，查询两个结点是否在同一棵树中，连接两棵树。

抽象一点地说，维护一堆集合，查询两个元素是否属于同一集合，合并两个集合。

其中，查询两点是否连通和连接两点可以使用并查集维护。

/*
并查集是一种支持查找一个元素所属的集合以及两个元素各自所属集合的合并等运算的数据结构。并查集的一种最简单实现就是维护数组v[n]，数组元素v[i]代表序号为i的顶点所属的集合的编号。初始状态时数组元素v[i]的值即为i。当两个顶点的集合编号不同时，将这两个顶点所构成的边加入到生成树中一定不会形成回路。当这条边被加入到生成树后，需要对这两个顶点所属的集合进行合并，也就是将两个顶点集合的编号统一。
*/
int v[N];
struct node{
    int x1;
    int x2;
    int weight;
    
} enc[N]; //按边的权值排好序的边集

void Kruskal()
{
    for(int i = 0; i < len; i++){
        v[i] = i;
    }
    
    while(++count < len){ //遍历全部的边
        int p1 = enc[k].x1;
        int p2 = enc[k].x2;
        
        if(v[p1] != v[p2]){
            count++;
            int q1 = v[p1];
            int q2 = v[p2];
            for(int i = 0; i < len; i++){
                if(v[i] == q1) v[i] = q2;
            }
        }
        
        k++;
    }
}

克鲁斯卡尔的时间复杂度

它主要分为三个部分，首先我们要对 n个节点进行初始化，所以第一部分的复杂度为O(n) ；然后，我们要对所有边 e 进行排序，用基于比较的排序算法，我们最快能够达到 eloge 的复杂度；最后，我们判断两个节点是否属于一个集合，由于树的高度和节点数呈现一个近似对数关系，而我们要对 n-1 条边进行判断，因此这一部分的时间复杂度就为nlogn 。由于在比较稠密的图中，边的个数大于节点的个数，所以总的复杂度我们取较大的eloge 。