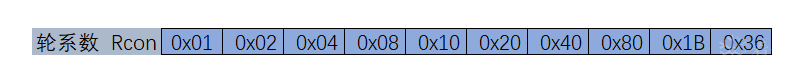常见加密算法

Tea加密及其变种

注意Tea，xTea和xxTea都是分组算法，输入会被分为以若干个字节组成的组元，逆向时要注意类型的转换

若寄存器溢出还得加上&0xffffffff

Tea

在密码学中，微型加密算法（Tiny Encryption Algorithm，TEA）是一种易于描述和执行的块密码，通常只需要很少的代码就可实现。

代码样例

#include <stdio.h>  
#include <stdint.h>  
  
//加密函数  
void encrypt (uint32_t* v, uint32_t* k) {  
    uint32_t v0=v[0], v1=v[1], sum=0, i;           /* set up */  
    uint32_t delta=0x9e3779b9;                     //magic number
    uint32_t k0=k[0], k1=k[1], k2=k[2], k3=k[3];   /* cache key */  
    for (i=0; i < 32; i++) {                       /* basic cycle start */  
        sum += delta;  
        v0 += ((v1<<4) + k0) ^ (v1 + sum) ^ ((v1>>5) + k1);  
        v1 += ((v0<<4) + k2) ^ (v0 + sum) ^ ((v0>>5) + k3);  
    }                                              /* end cycle */  
    v[0]=v0; v[1]=v1;  
}  
//解密函数  
void decrypt (uint32_t* v, uint32_t* k) {  
    uint32_t v0=v[0], v1=v[1], sum=0xC6EF3720, i;  //sum = 次数 * magic number
    uint32_t delta=0x9e3779b9;                     //magic number 
    uint32_t k0=k[0], k1=k[1], k2=k[2], k3=k[3];   /* cache key */  
    for (i=0; i<32; i++) {                         /* basic cycle start */  
        v1 -= ((v0<<4) + k2) ^ (v0 + sum) ^ ((v0>>5) + k3);  
        v0 -= ((v1<<4) + k0) ^ (v1 + sum) ^ ((v1>>5) + k1);  
        sum -= delta;  
    }                                              /* end cycle */  
    v[0]=v0; v[1]=v1;  
}  

int main()  
{  
    uint32_t v[2]={1,2},k[4]={2,2,3,4};  
    // v为要加密的数据是两个32位无符号整数  
    // k为加密解密密钥，为4个32位无符号整数，即密钥长度为128位  
    printf("加密前原始数据：%u %u\n",v[0],v[1]);  
    encrypt(v, k);  
    printf("加密后的数据：%u %u\n",v[0],v[1]);  
    decrypt(v, k);  
    printf("解密后的数据：%u %u\n",v[0],v[1]);  
    return 0;  
}

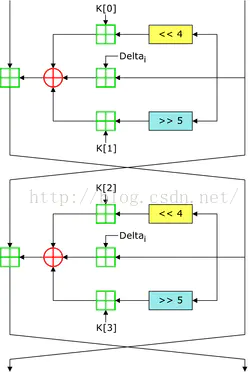
TEA算法有64位的明文，128位的密钥以及一个常数 $\delta$ 组成。$\delta$源自于黄金比例，但它的数值的精确度并不重要，于是被定义为 $\delta$=「($\tilde{A}$5 - 1)231」(即程序里面的0×9E3779B9)

TEA是将明文每64位位一组进行加密，每次加密将这64位分为两部分，高32位和低32位(后面分别用Mup和Mdown来表示)，而密钥(Key)则拆分为4部分。

一般的轮数是32或64（8的倍数），加密后将结果覆写回去

注意，x-=0x61c88647和x+=0x9e3779b9，这两个值是等价的，可能会在反汇编中看到

这里将上面测试的代码编译好拖入IDA中进行观察

可以看到δ就被反编译为v4 -= 1640531527;

代码样例

#include <cstdio>
#include <cstdint>

using namespace std;

void decrypt(unsigned long* EntryData, unsigned long* Key)
{
    unsigned long Mup = EntryData[0];
    unsigned long Mdown = EntryData[1];

    unsigned long sum = 0;
    unsigned long delta = 0xD33B470;
 	int n=32;
        
   	sum = delta*n; //视次数.
    
    for(int i=0;i<n;i++){
        Mdown -= ((Mup << 4) + Key[2]) ^ (Mup + sum) ^ ((Mup >> 5) + Key[3]);
        Mup -= ((Mdown << 4) + Key[0]) ^ (Mdown + sum) ^ ((Mdown >> 5) + Key[1]);
        sum -= delta;
    }
    
    EntryData[0] = Mup;
    EntryData[1] = Mdown;
}

int main()
{
    unsigned long key[] = {1,2,3,4};
    unsigned long EntryData[] = {0x89546517, 0x324665ed};
    decrypt(EntryData, key);
    for (int j = 0; j < 2; j++) {                      
            for (int k = 0; k < 4; k++) {
                printf("%c", EntryData[j] & 0xff);
                EntryData[j] >>= 8;
            }
        }
    return 0;
}

//
//    
//0x89546517, 0x324665ed  0xfda9583d, 0x97615ee2 0x91f160e4, 0xa2e9e973  0x999acb59, 0x7de1b1ec
//moectf{Th3_TEA_!S_s0_t4s7y~~!!!}

xTea

xTea算法是Tea的升级版，加入了位移和异或运算，和更多的密钥表

#include <stdio.h>  
#include <stdint.h>  
  
/* take 64 bits of data in v[0] and v[1] and 128 bits of key[0] - key[3] */  
  
void encipher(unsigned int num_rounds, uint32_t v[2], uint32_t const key[4]) {  
    unsigned int i;  
    uint32_t v0=v[0], v1=v[1], sum=0, delta=0x9E3779B9;  
    for (i=0; i < num_rounds; i++) {  
        v0 += (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]);  
        sum += delta;  
        v1 += (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum>>11) & 3]);  
    }  
    v[0]=v0; v[1]=v1;  
}  
  
void decipher(unsigned int num_rounds, uint32_t v[2], uint32_t const key[4]) {  
    unsigned int i;  
    uint32_t v0=v[0], v1=v[1], delta=0x9E3779B9, sum=delta*num_rounds;  
    for (i=0; i < num_rounds; i++) {  
        v1 -= (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum>>11) & 3]);  
        sum -= delta;  
        v0 -= (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]);  
    }  
    v[0]=v0; v[1]=v1;  
}  
  
int main()  
{  
    uint32_t v[2]={1,2};  
    uint32_t const k[4]={2,2,3,4};  
    unsigned int r=32;//num_rounds建议取值为32  
    // v为要加密的数据是两个32位无符号整数  
    // k为加密解密密钥，为4个32位无符号整数，即密钥长度为128位  
    printf("加密前原始数据：%u %u\n",v[0],v[1]);  
    encipher(r, v, k);  
    printf("加密后的数据：%u %u\n",v[0],v[1]);  
    decipher(r, v, k);  
    printf("解密后的数据：%u %u\n",v[0],v[1]);  
    return 0;  
}

整体逆向和Tea差不太大

xxTea

xxTEA，又称Corrected Block TEA

特点：原字符串长度可以不是4的倍数了


  #define MX (z>>5^y<<2) + (y>>3 ^ z<<4)^(sum^y) + (k[ i&3 ^ e] ^ z);
 
  long btea(long* v, long n, long* k) {
    unsigned long z=v[n-1], y=v[0], sum=0, e, DELTA=0x9e3779b9;
    long i, q ;
    if (n > 1) {         
      q = 6 + 52/n;
      while (q-- > 0) {
        sum += DELTA;
        e = (sum >> 2) & 3;
        for (i=0; i<n-1; i++){ 
            y = v[i+1];
            z = v[i] += MX;
        } 
        y = v[0];
        z = v[n-1] += MX;
      }
      return 0 ;
    } 
      
      
      else if (n < -1) { 
      n = -n;
      q = 6 + 52/n;
      sum = q*DELTA ;
      while (sum != 0) {
        e = (sum >> 2) & 3;
        for (i=n-1; i>0; i--) {
            z = v[i-1];
            y = v[i] -= MX;   
        }
        z = v[n-1];
        y = v[0] -= MX;
        sum -= DELTA;
      }
      return 0;
    }
    return 1;
  }
/*
 long btea(long* v, long n, long* k)
 
v是要加密的组元的起始地址，以32bit为单位，这里用long来实现。

n是要加密的组元个数，正数是加密，负数是解密。

k是密钥的起始地址，长度为4个组元，4*32=128bit。

返回值为0或1（对应n=0，没有计算）。

加密的结果会直接写回到v中。
*/

Base64

Base64 是一种基于 64 个可打印字符来表示二进制数据的表示方法。

特征：由64个字符(A-Z,a-z,0-9,+,/)组成，末尾可能会出现1或2个’=’ 最多有2个

对二进制数据以6个位(bit)为一组切分，所以分切之前的二进制位数应该是24的倍数（即6，8的最小公倍数）。如果不足24位,则在编码后数据后面添加”=”

转换的时候，将 3 字节的数据，先后放入一个 24 位的缓冲区中，先来的字节占高位。数据不足 3 字节的话，于缓冲器中剩下的比特用 0 补足。每次取出 6 比特，按照其值选择ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/中的字符作为编码后的输出，直到全部输入数据转换完成。

通常而言 Base64 的识别特征为索引表，当我们能找到 ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/ 这样索引表，再经过简单的分析基本就能判定是 Base64 编码。

当然，有些题目 base64 的索引表是会变的，一些变种的 base64 主要就是修改了这个索引表。

文本:        V        a        n
ASCII:      86       97      110
Bin:    010101|10 0110|0001 01|101110
6位一组：  21      38      5      46 
Base64:   V       m       F      u

# 码表
s = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/" 


def My_base64_encode(inputs):
    # 将字符串转化为2进制
    bin_str = []
    for i in inputs:
        x = str(bin(ord(i))).replace('0b', '')
        bin_str.append('{:0>8}'.format(x))
    # print(bin_str)
    # 输出的字符串
    outputs = ""
    # 不够三倍数，需补齐的次数
    nums = 0
    while bin_str:
        # 每次取三个字符的二进制
        temp_list = bin_str[:3]
        if (len(temp_list) != 3):
            nums = 3 - len(temp_list)
            while len(temp_list) < 3:
                temp_list += ['0' * 8]
        temp_str = "".join(temp_list)
        # print(temp_str)
        # 将三个8字节的二进制转换为4个十进制
        temp_str_list = []
        for i in range(0, 4):
            temp_str_list.append(int(temp_str[i * 6:(i + 1) * 6], 2))
        # print(temp_str_list)
        if nums:
            temp_str_list = temp_str_list[0:4 - nums]

        for i in temp_str_list:
            outputs += s[i]
        bin_str = bin_str[3:]
    outputs += nums * '='
    print("Encrypted String:\n%s " % outputs)


def My_base64_decode(inputs):
    # 将字符串转化为2进制
    bin_str = []
    for i in inputs:
        if i != '=':
            x = str(bin(s.index(i))).replace('0b', '')
            bin_str.append('{:0>6}'.format(x))
    # print(bin_str)
    # 输出的字符串
    outputs = ""
    nums = inputs.count('=')
    while bin_str:
        temp_list = bin_str[:4]
        temp_str = "".join(temp_list)
        # print(temp_str)
        # 补足8位字节
        if (len(temp_str) % 8 != 0):
            temp_str = temp_str[0:-1 * nums * 2]
        # 将四个6字节的二进制转换为三个字符
        for i in range(0, int(len(temp_str) / 8)):
            outputs += chr(int(temp_str[i * 8:(i + 1) * 8], 2))
        bin_str = bin_str[4:]
    print("Decrypted String:\n%s " % outputs)


print()
print("     *************************************")
print("     *    (1)encode         (2)decode    *")
print("     *************************************")
print()

num = input("Please select the operation you want to perform:\n")
if (num == "1"):
    input_str = input("Please enter a string that needs to be encrypted: \n")
    My_base64_encode(input_str)
else:
    input_str = input("Please enter a string that needs to be decrypted: \n")
    My_base64_decode(input_str)

哈希函数

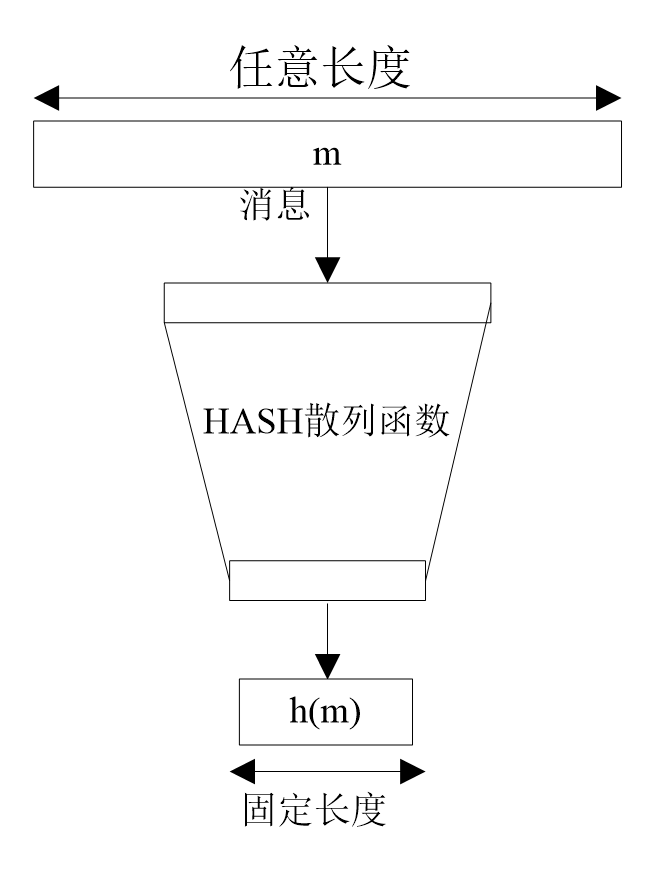
哈希函数（Hash Function）把消息或数据压缩成摘要，使得数据量变小。

显然对于任何一个 hash 值，理论上存在若干个消息与之对应，即碰撞。

目前的 Hash 函数主要有 MD5，SHA1，SHA256，SHA512。目前的大多数 hash 函数都是迭代性的，即使用同一个 hash 函数，不同的参数进行多次迭代运算。

算法类型	输出hash值的长度
MD5	128bit
SHA1	160bit
SHA256	256bit
SHA512	512bit

MD5

MD5 消息摘要算法（英语：MD5 Message-Digest Algorithm），一种被广泛使用的密码散列函数，可以产生出一个 128 位（16 字节）的散列值（hash value），用于确保信息传输完整一致。MD5 由美国密码学家罗纳德 · 李维斯特（Ronald Linn Rivest）设计，于 1992 年公开，用以取代 MD4 算法。这套算法的程序在 RFC 1321 中被加以规范。

MD5编码具有单向性，即由明文变密文简单，由密文变明文困难。基于这个特性，MD5可以有效保证信息的完整性，常用于验证数据是否被篡改

MD5是不可逆的算法，同一个MD5的值对应无数种密文

MD5码以512位分组来处理输入的信息，且每一分组又被划分为16个32位子分组，经过了一系列的处理后，算法的输出由4个32位分组组成，并级联后将生成一个128位散列值。
继续向后取512位数据，不够则进行填充。每次的运算都由前一轮的128位散列值和当前的512bit值进行运算
因此MD5结果值是一段固定长度的数据，无论原始数据是多长或多短，其MD5值都是128bit
最后按十六进制计算输出，即结果为0-9a-f

伪代码

/Note: All variables are unsigned 32 bits and wrap modulo 2^32 when calculating
var int[64] r, k

//r specifies the per-round shift amounts
r[ 0..15]：= {7, 12, 17, 22,  7, 12, 17, 22,  7, 12, 17, 22,  7, 12, 17, 22} 
r[16..31]：= {5,  9, 14, 20,  5,  9, 14, 20,  5,  9, 14, 20,  5,  9, 14, 20}
r[32..47]：= {4, 11, 16, 23,  4, 11, 16, 23,  4, 11, 16, 23,  4, 11, 16, 23}
r[48..63]：= {6, 10, 15, 21,  6, 10, 15, 21,  6, 10, 15, 21,  6, 10, 15, 21}

//Use binary integer part of the sines of integers as constants:
for i from 0 to 63
    k[i] := floor(abs(sin(i + 1)) × 2^32)

//Initialize variables:
var int h0 := 0x67452301
var int h1 := 0xEFCDAB89
var int h2 := 0x98BADCFE
var int h3 := 0x10325476

//Pre-processing:
append "1" bit to message
append "0" bits until message length in bits ≡ 448 (mod 512)
append bit length of message as 64-bit little-endian integer to message

//Process the message in successive 512-bit chunks:
for each 512-bit chunk of message
    break chunk into sixteen 32-bit little-endian words w[i], 0 ≤ i ≤ 15

    //Initialize hash value for this chunk:
    var int a := h0
    var int b := h1
    var int c := h2
    var int d := h3

    //Main loop:
    for i from 0 to 63
        if 0 ≤ i ≤ 15 then
            f := (b and c) or ((not b) and d)
            g := i
        else if 16 ≤ i ≤ 31
            f := (d and b) or ((not d) and c)
            g := (5×i + 1) mod 16
        else if 32 ≤ i ≤ 47
            f := b xor c xor d
            g := (3×i + 5) mod 16
        else if 48 ≤ i ≤ 63
            f := c xor (b or (not d))
            g := (7×i) mod 16

        temp := d
        d := c
        c := b
        b := leftrotate((a + f + k[i] + w[g]),r[i]) + b
        a := temp
    Next i
    //Add this chunk's hash to result so far:
    h0 := h0 + a
    h1 := h1 + b 
    h2 := h2 + c
    h3 := h3 + d
End ForEach
var int digest := h0 append h1 append h2 append h3 //(expressed as little-endian)

特征

h0 = 0x67452301;
h1 = 0xefcdab89;
h2 = 0x98badcfe;
h3 = 0x10325476;

攻击方法

上网站碰撞

RC4

RC4是一种流加密算法，密钥长度可变，加解密使用相同的密钥，算是对称加密算法

void rc4_init(unsigned char *s, unsigned char *key, unsigned long Len) //初始化函数
{
    int i =0, j = 0;
    char k[256] = {0};
    unsigned char tmp = 0;
    for (i=0;i<256;i++) {
        s[i] = i;
        k[i] = key[i%Len];
    }
    for (i=0; i<256; i++) {
        j=(j+s[i]+k[i])%256;
        tmp = s[i];
        s[i] = s[j]; //交换s[i]和s[j]
        s[j] = tmp;
    }
 }

void rc4_crypt(unsigned char *s, unsigned char *Data, unsigned long Len) //加解密
{
    int i = 0, j = 0, t = 0;
    unsigned long k = 0;
    unsigned char tmp;
    for(k=0;k<Len;k++) {
        i=(i+1)%256;
        j=(j+s[i])%256;
        tmp = s[i];
        s[i] = s[j]; //交换s[x]和s[y]
        s[j] = tmp;
        t=(s[i]+s[j])%256;
        Data[k] ^= s[t];
     }
} 
//每收到一个字节，就进行循环。通过一定的算法定位 S 盒中的一个元素，并与输入字节异或，得到 k。循环中还改变了 S 盒。如果输入的是明文，输出的就是密文；如果输入的是密文，输出的就是明文。

RC4 主要包含三个流程

初始化 S 和 T 数组。
初始化置换 S。
生成密钥流。

初始化S,T数组

for (i=0;i<256;i++) {
        s[i] = i;
        k[i] = key[i%Len];
    }

置换

for (i=0; i<256; i++) {
       j=(j+s[i]+k[i])%256;
       tmp = s[i];
       s[i] = s[j]; //交换s[i]和s[j]
       s[j] = tmp;
   }

生成流密钥，并处理Data

for(k=0;k<Len;k++) {
        i=(i+1)%256;
        j=(j+s[i])%256;
        tmp = s[i];
        s[i] = s[j]; //交换s[x]和s[y]
        s[j] = tmp;
        t=(s[i]+s[j])%256;
        Data[k] ^= s[t];
     }

由于异或运算的对合性，RC4 加密解密使用同一套算法

RSA

AES

高级加密标准（英语：Advanced Encryption Standard，缩写AES)，在密码学中又称Rijndael加密法，是美国联邦政府采用的一种区块加密标准。这个标准用来替代原先的DES，已经被多方分析且广为全世界所使用。经过五年的甄选流程，高级加密标准由美国国家标准与技术研究院（NIST）于2001年11月26日发布于FIPS PUB 197，并在2002年5月26日成为有效的标准。2006年，高级加密标准已然成为对称密钥加密中最流行的算法之一。

对称加密，即加密与解密用的是同一套密钥

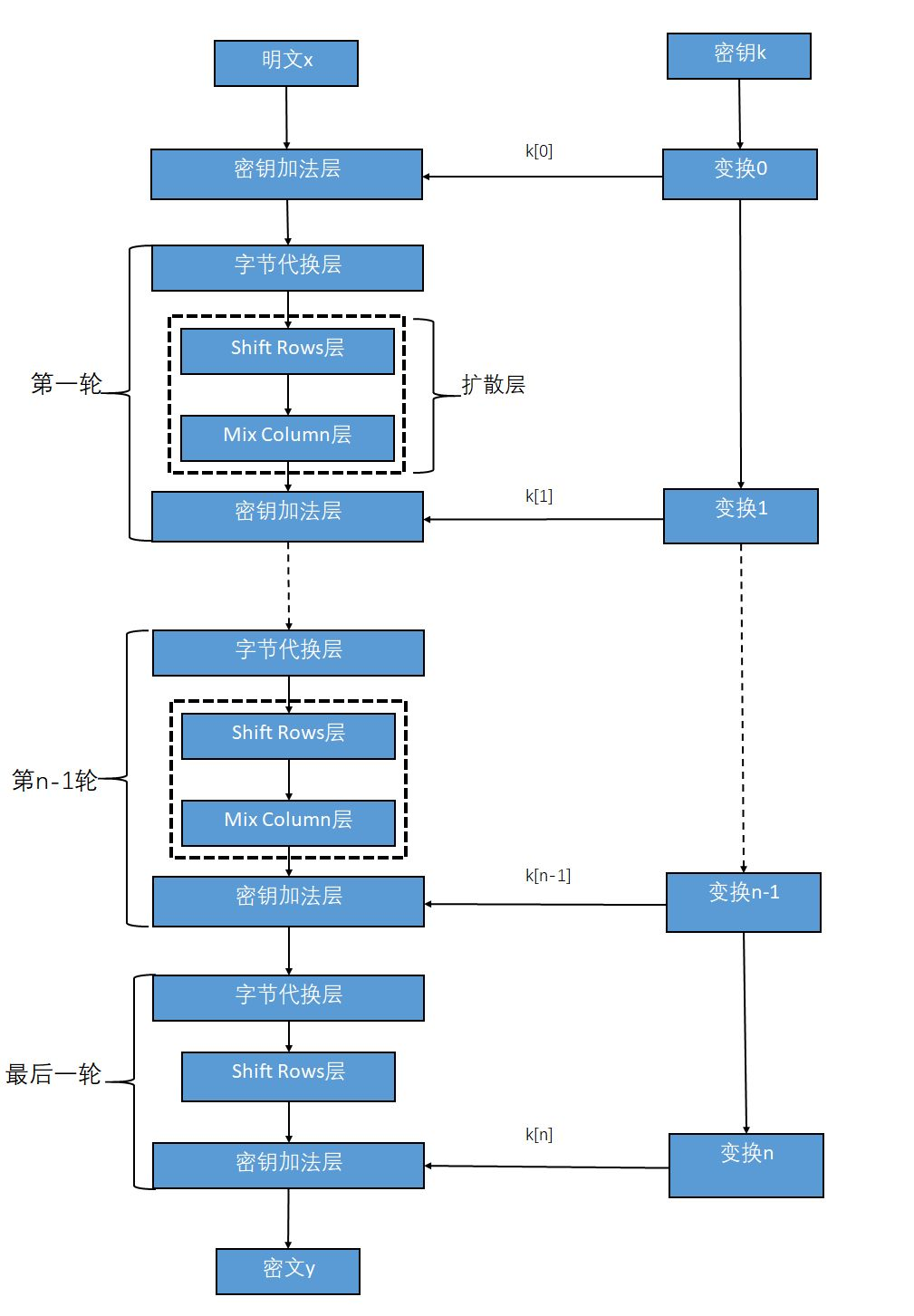
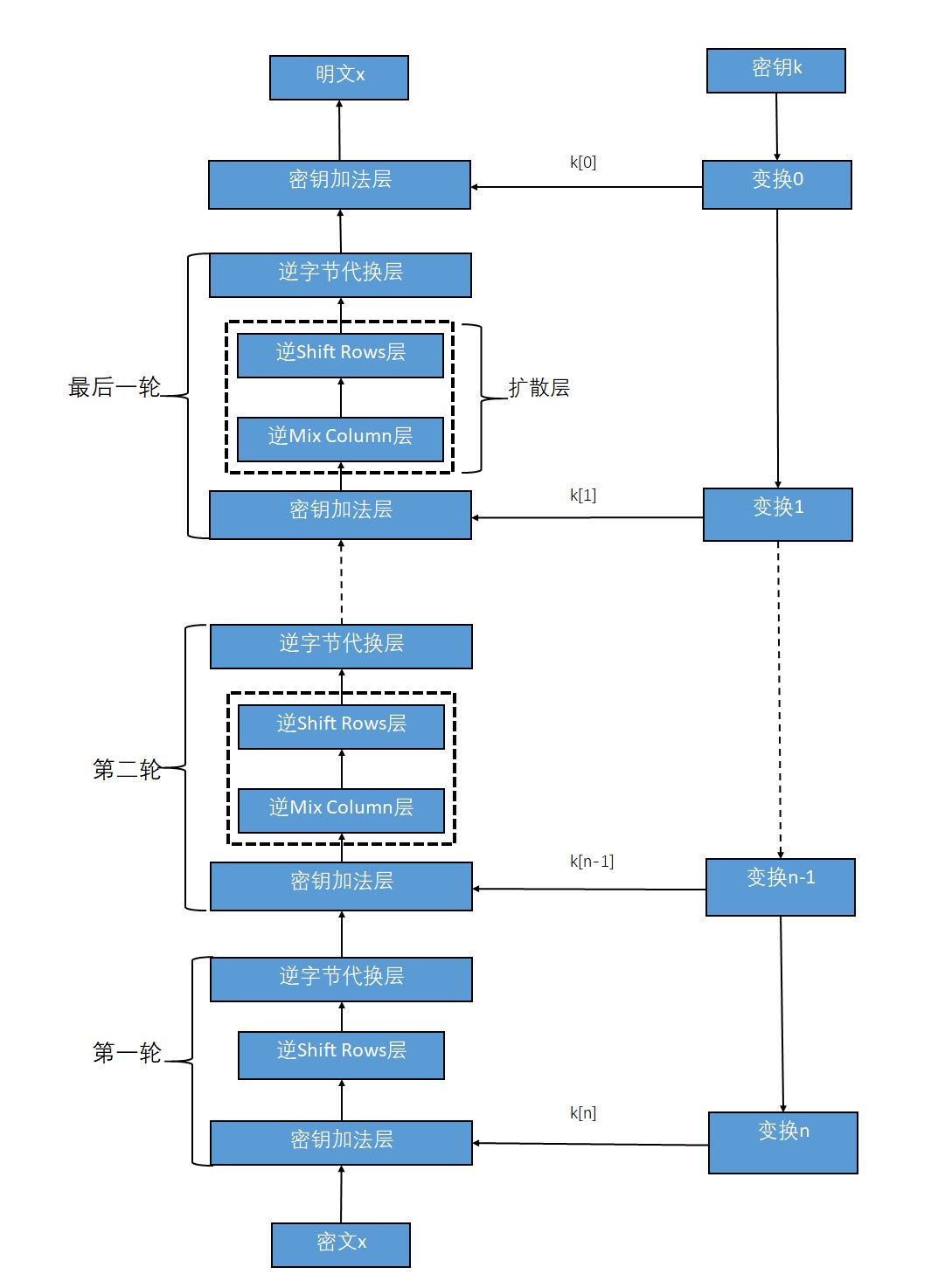
AES算法主要有四种操作处理，分别是密钥加法层(也叫轮密钥加，英文Add Round Key)、字节代换层(SubByte)、行位移层(Shift Rows)、列混淆层(Mix Column)。而明文x和密钥k都是由16个字节组成的数据(当然密钥还支持192位和256位的长度，暂时不考虑)，它是按照字节的先后顺序从上到下、从左到右进行排列的。而加密出的密文读取顺序也是按照这个顺序读取的，相当于将数组还原成字符串的模样了，然后再解密的时候又是按照4·4数组处理的。

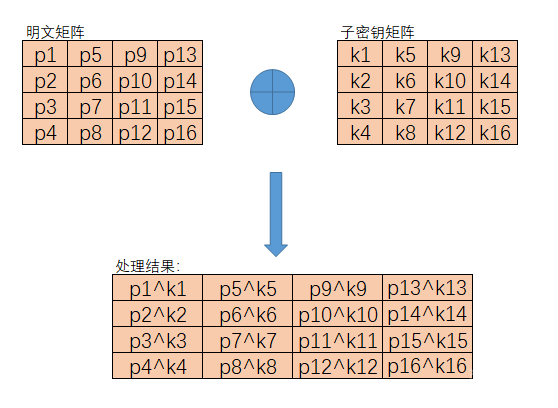
密钥加法层

在密钥加法层中有两个输入的参数，分别是明文和子密钥k[0]，而且这两个输入都是128位的。k[0]实际上就等同于密钥k。

在扩展域中加减法操作和异或运算等价，将两个输入的数据进行按字节异或操作就会得到运算的结果。

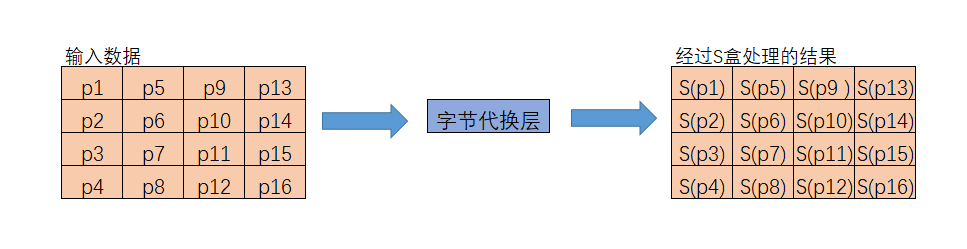
字节代换层

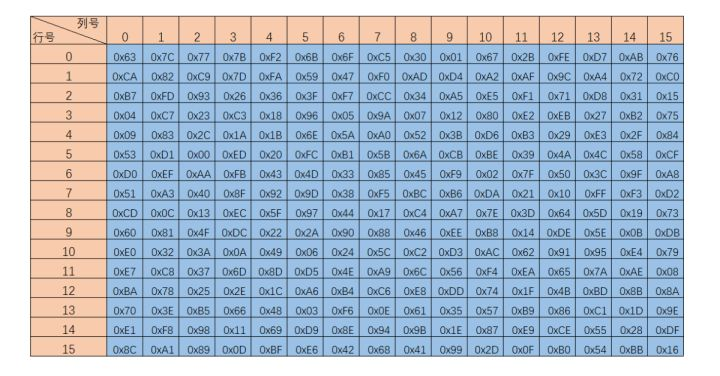
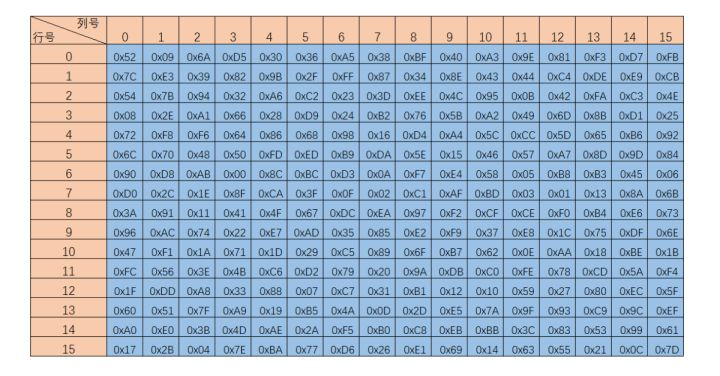
字节代换层的主要功能就是让输入的数据通过S_box表完成从一个字节到另一个字节的映射，这里的S_box表是通过某种方法计算出来的，具体的计算方法将在进阶部分进行介绍，我们基础部分就只给出计算好的S_box结果。S_box表是一个拥有256个字节元素的数组，可以将其定义为一维数组，也可以将其定义为16·16的二维数组，如果将其定义为二维数组，读取S_box数据的方法就是要将输入数据的每个字节的高四位作为第一个下标，第四位作为第二个下标，略有点麻烦。这里建议将其视作一维数组即可。逆S盒与S盒对应，用于解密时对数据处理，我们对解密时的程序处理称作逆字节代换，只是使用的代换表盒加密时不同而已。

S盒

逆S盒

加密图示：

行位移——ShiftRows

行位移操作最为简单，它是用来将输入数据作为一个4·4的字节矩阵进行处理的，然后将这个矩阵的字节进行位置上的置换。ShiftRows子层属于AES手动的扩散层，目的是将单个位上的变换扩散到影响整个状态当，从而达到雪崩效应。在加密时行位移处理与解密时的处理相反，我们这里将解密时的处理称作逆行位移。它之所以称作行位移，是因为它只在4·4矩阵的行间进行操作，每行4字节的数据。在加密时，保持矩阵的第一行不变，第二行向左移动8Bit(一个字节)、第三行向左移动2个字节、第四行向左移动3个字节。而在解密时恰恰相反，依然保持第一行不变，将第二行向右移动一个字节、第三行右移2个字节、第四行右移3个字节。操作结束！

正向行位移图解:

逆向行位移图解:

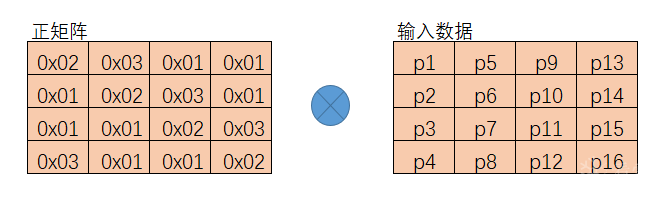
列混淆——MixColumn

列混淆子层是AES算法中最为复杂的部分，属于扩散层，列混淆操作是AES算法中主要的扩散元素，它混淆了输入矩阵的每一列，使输入的每个字节都会影响到4个输出字节。行位移子层和列混淆子层的组合使得经过三轮处理以后，矩阵的每个字节都依赖于16个明文字节成可能。其中包含了矩阵乘法、伽罗瓦域内加法和乘法的相关知识。

在加密的正向列混淆中，我们要将输入的4·4矩阵左乘一个给定的4·4矩阵。而它们之间的加法、乘法都在扩展域GF(2^8)中进行。

列混淆的代码

const unsigned char MixArray[4][4] = {
    0x02, 0x03, 0x01, 0x01,
    0x01, 0x02, 0x03, 0x01,
    0x01, 0x01, 0x02, 0x03,
    0x03, 0x01, 0x01, 0x02};
int MixColum(unsigned char(*PlainArray)[4])`
{
    int ret = 0;
    //定义变量
    unsigned char ArrayTemp[4][4];
    //初始化变量
    memcpy(ArrayTemp, PlainArray, 16);
    //矩阵乘法4*4
    for(int i = 0; i < 4; i++)
    {
        for (int j = 0; j < 4; j++)
        {
            PlainArray[i][j] = GaloisMultiplication(MixArray[i][0], ArrayTemp[0][j]) ^
                               GaloisMultiplication(MixArray[i][1], ArrayTemp[1][j]) ^
                               GaloisMultiplication(MixArray[i][2], ArrayTemp[2][j]) ^
                               GaloisMultiplication(MixArray[i][3], ArrayTemp[3][j]);
        }
    }
	return ret;
}

我们发现在矩阵乘法中，出现了加法和乘法运算，在扩展域中加法操作等同于异或运算，而乘法操作需要一个特殊的方式进行处理，于是我们就先把代码中的加号换成异或符号，然后将伽罗瓦域的乘法定义成一个有两个参数的函数，并让他返回最后计算结果。于是列混淆的代码就会变成下面的样子：

///////////////////////////////////////////////////////////////`
//功能: 伽罗瓦域内的乘法运算 GF(128)
//参数: Num_L 输入的左参数
//Num_R 输入的右参数
//返回值:计算结果
char GaloisMultiplication(unsigned char Num_L, unsigned char Num_R)
{
    //定义变量
    unsigned char Result = 0; //伽罗瓦域内乘法计算的结果
    while(Num_L)
    {
        //如果Num_L最低位是1就异或Num_R，相当于加上Num_R * 1
        if(Num_L & 0x01)
        {
        Result ^= Num_R;
        }
        //Num_L右移一位，相当于除以2
        Num_L = Num_L >> 1;
        //如果Num_R最高位为1
        if(Num_R & 0x80)
        {
            //左移一位相当于乘二
            Num_R = Num_R << 1;//注：这里会丢失最高位，但是不用担心
            Num_R ^= 0x1B;//计算伽罗瓦域内除法Num_R = Num_R/(x^8(刚好丢失最高位) +x^4+x^3+x^1+1)
        }
        else
        {
            //左移一位相当于乘二
            Num_R = Num_R << 1;
        }
    }
    return Result;
}

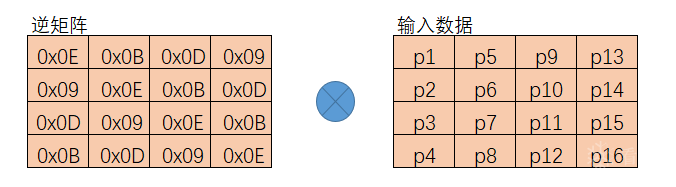
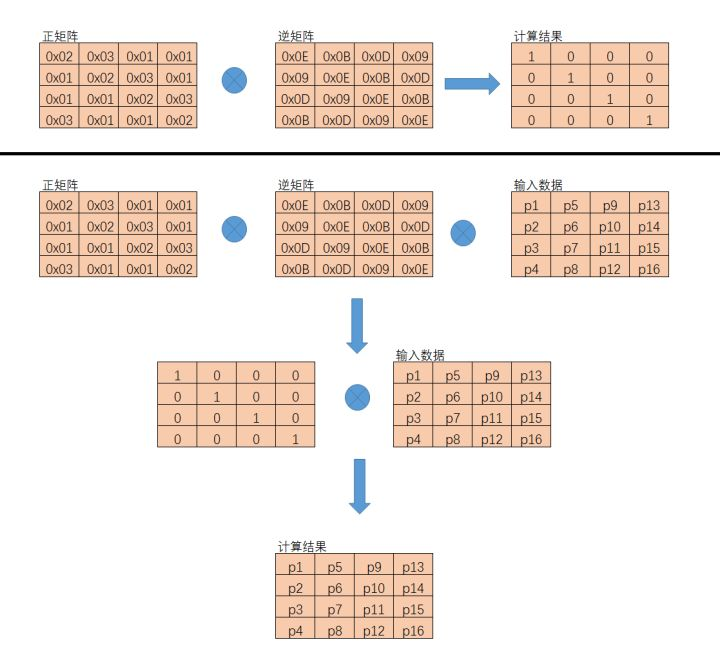
在解密的逆向列混淆中与正向列混淆的不同之处在于使用的左乘矩阵不同，它与正向列混淆的左乘矩阵互为逆矩阵，也就是说，数据矩阵同时左乘这两个矩阵后，数据矩阵不会发生任何变化。

正向列混淆处理

逆向列混淆

加解密验证

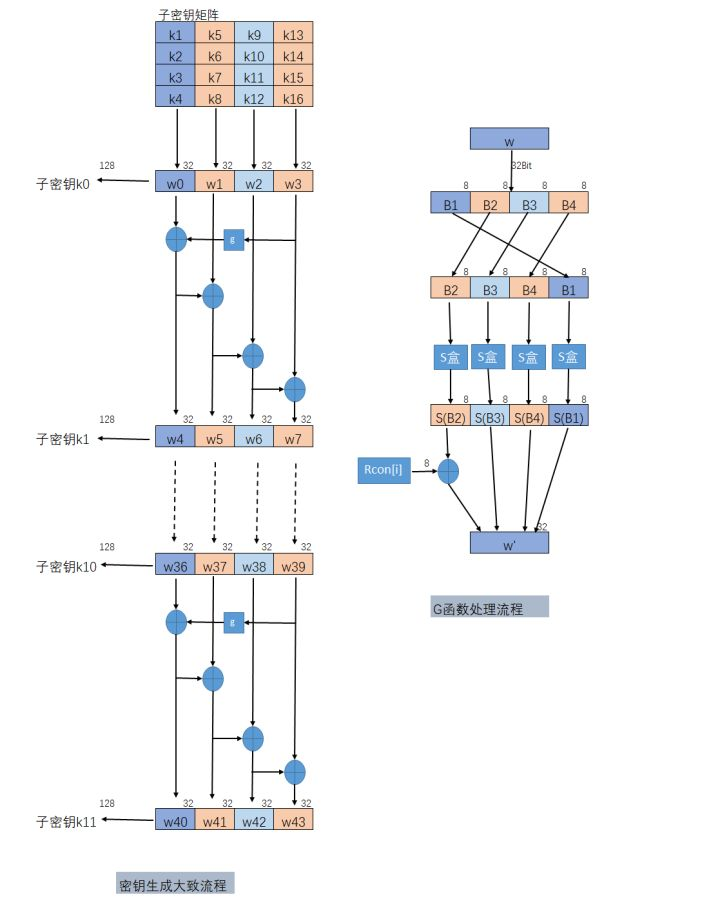
AES密钥生成

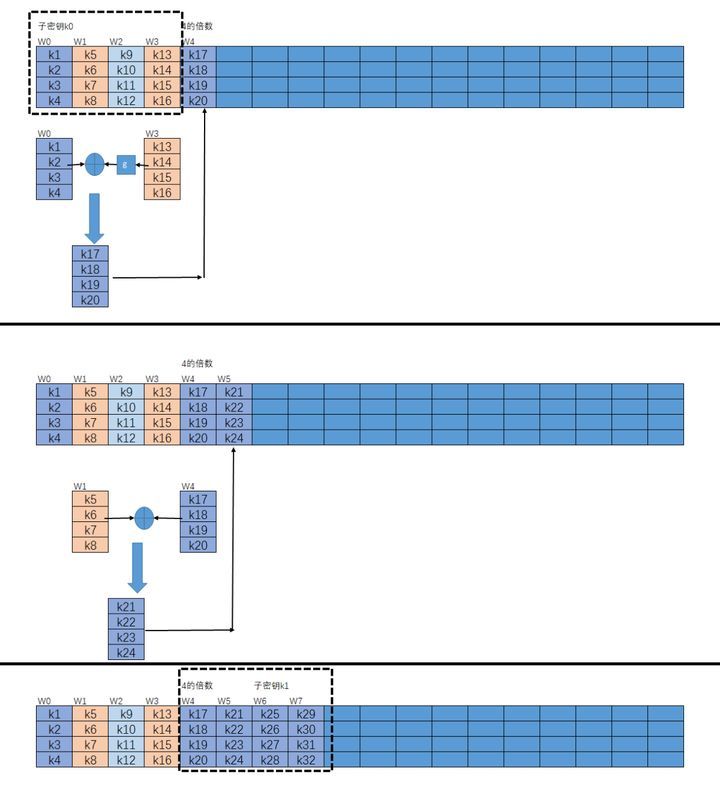
子密钥的生成是以列为单位进行的，一列是32Bit，四列组成子密钥共128Bit。生成子密钥的数量比AES算法的轮数多一个，因为第一个密钥加法层进行密钥漂白时也需要子密钥。密钥漂白是指在AES的输入盒输出中都使用的子密钥的XOR加法。子密钥在图中都存储在W[0]、W[1]、…、W[43]的扩展密钥数组之中。k1-k16表示原始密钥对应的字节，而图中子密钥k0与原始子密钥相同。在生成的扩展密钥中W的下标如果是4的倍数时(从零开始)需要对异或的参数进行G函数处理。扩展密钥生成有关公式如下：

1<= i <= 10
1<= j <= 3
w[4i] = W[4(i-1)] + G(W[4i-1]);
w[4i+j] = W[4(i-1)+j] + W[4i-1+j];

函数G()首先将4个输入字节进行翻转，并执行一个按字节的S盒代换，最后用第一个字节与轮系数Rcon进行异或运算。轮系数是一个有10个元素的一维数组，一个元素1个字节。G()函数存在的目的有两个，一是增加密钥编排中的非线性；二是消除AES中的对称性。这两种属性都是抵抗某些分组密码攻击必要的。

生成密钥代码:

//用于密钥扩展 Rcon[0]作为填充，没有实际用途
const unsigned int Rcon[11] = { 0x00, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1B, 0x36 };
int Key_S_Substitution(unsigned char(*ExtendKeyArray)[44], unsigned int nCol)
{
    int ret = 0;
    for (int i = 0; i < 4; i++)
    {
    	ExtendKeyArray[i][nCol] = S_Table[(ExtendKeyArray[i][nCol]) >> 4][(ExtendKeyArray[i][nCol]) & 0x0F];
    }
    return ret;
}

int G_Function(unsigned char(*ExtendKeyArray)[44], unsigned int nCol)
{
    int ret = 0;
    //1、将扩展密钥矩阵的nCol-1列复制到nCol列上，并将nCol列第一行的元素移动到最后一行，其他行数上移一行
    for (int i = 0; i < 4; i++)
    {
    	ExtendKeyArray[i][nCol] = ExtendKeyArray[(i + 1) % 4][nCol - 1];
    }
    //2、将nCol列进行S盒替换
    Key_S_Substitution(ExtendKeyArray, nCol);
    //3、将该列第一行元素与Rcon进行异或运算
    ExtendKeyArray[0][nCol] ^= Rcon[nCol / 4];
    return ret;
}

int CalculateExtendKeyArray(const unsigned char(*PasswordArray)[4], unsigned char(*ExtendKeyArray)[44])
{
    int ret = 0;
    //1、将密钥数组放入前四列扩展密钥组
    for (int i = 0; i < 16; i++)
    {
    	ExtendKeyArray[i & 0x03][i >> 2] = PasswordArray[i & 0x03][i >> 2];
    }
    
    //2、计算扩展矩阵的后四十列
    for (int i = 1; i < 11; i++) //进行十轮循环
    {
        //(1)如果列号是4的倍数，这执行G函数 否则将nCol-1列复制到nCol列上
        G_Function(ExtendKeyArray, 4*i);
        
        //(2)每一轮中，各列进行异或运算
        // 列号是4的倍数
        for (int k = 0; k < 4; k++)//行号
        {
        	ExtendKeyArray[k][4 * i] = ExtendKeyArray[k][4 * i] ^ ExtendKeyArray[k][4 * (i - 1)];
        }
        // 其他三列
        for (int j = 1; j < 4; j++)//每一轮的列号
        {
            for (int k = 0; k < 4; k++)//行号
            {
            	ExtendKeyArray[k][4 * i + j] = ExtendKeyArray[k][4 * i + j - 1] ^ ExtendKeyArray[k][4 * (i - 1) + j];
            }
        }
    }
    return ret;
}

AES解密

脚本建议直接使用py的第三方库

from Crypto.Cipher import AES
from Crypto.Util.number import *
key = long_to_bytes(0xcb8d493521b47a4cc1ae7e62229266ce)
mi = long_to_bytes(0xbc0aadc0147c5ecce0b140bc9c51d52b46b2b9434de5324bad7fb4b39cdb4b5b)
lun = AES.new(key, mode=AES.MODE_ECB)
flag = lun.decrypt(mi)
print(flag)